도형의 방정식 시작하기

1. 두 점 사이의 거리

 

수직선에서 두 점사이 거리 

수직선 상에서 두 점 A와 B 사이의 거리는 두 점의 좌표의 차이로 정의한다. 예를 들어 두 점 A와 B가 수직선 상에 있을 때, 좌표를 각각 x₁와 x₂라고 가정하면 두 점 사이의 거리는 다음과 같이 표현할 수 있다.

d(거리) = |x₂ - x₁|

즉, 두 점의 x 좌표의 차이를 절댓값으로 취한 값이 두 점 사이의 거리가 된다.

 

좌표평면에서 두 점사이 거리

 

유클리드 기하공간에서(모든 점들의 비중이 균일한) 좌표평면 상에서 두 점 사이의 거리는 피타고라스의 정리를 이용하여 정의되어 있다. 

 

옆의 그림에서 두 점의 좌표를 A(x₁, y₁)과 B(x₂, y₂)라고 했을 때, 두 점 사이의 거리 d는 다음과 같이 표현된다.

 

d = √((x₂ - x₁)² + (y₂ - y₁)²)

 

 

 

 

 

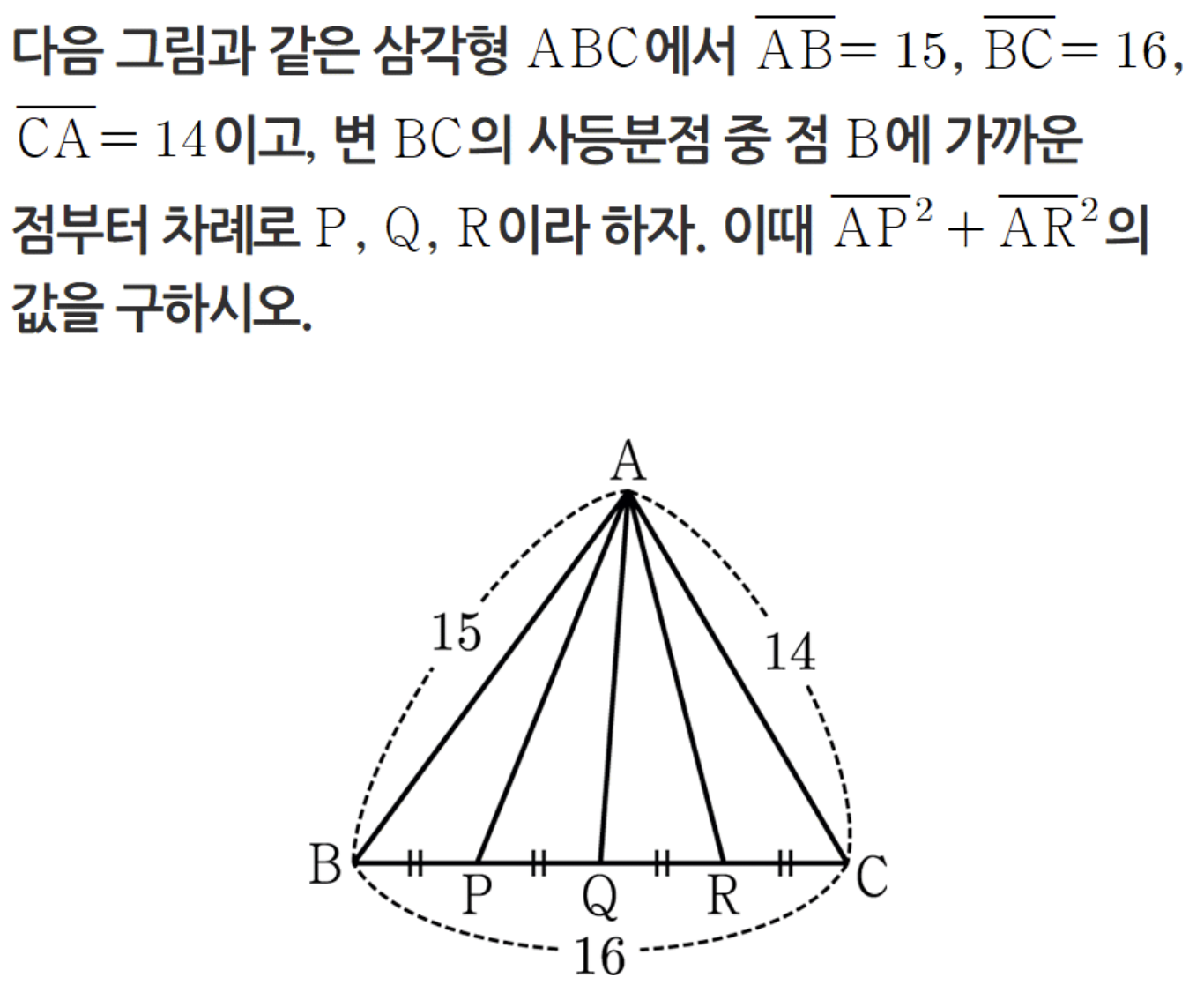
<예시>

이미지를 클릭하면 강의영상으로 연결됩니다.

이미지를 클릭하면 강의 영상으로 연결됩니다.

이미지를 클릭하면 강의 영상으로 연결됩니다.

이미지를 클릭하면 강의 영상으로 연결됩니다.

2. 파푸스 중선정리

삼각형의 한 꼭짓점과 대변의 중점을 이어 만들어지는 선분 사이에 2(선분 BD² + 선분 AD²) = 선분 AB² + 선분 AC² 를 만족하는 관계를 설명하는 정리로 증명은 위 그림을 통해 알 수 있다.

 

스튜어트 정리(Stewart's Theorem)

삼각형에서 세 변과 그에 대한 세 개의 선분 사이의 관계를 나타내는 정리로 이 정리는 삼각형 내에서 선분이 만나는 지점을 사용하여 세 개의 선분 사이의 관계식을 도출한다.

스튜어트 정리는 위 그림과 같이 표현될 수 있으며 삼각함수를 이용하지 않은 증명과정은 이미지를 클릭하면 영상을 통해 확인할 수 있다.

 

아폴리오니오스 정리(Apollonius' Theorem)

파푸스 중선정리와 같은 내용이며 평행사변형의 변의 길이관계식으로 유도할 수 있다.

 

<예시> 이미지를 클릭하면 풀이 영상으로 연결됩니다.

 

2021 학년도 9월 모의고사 나형 25번