삼각함수 시작하기 2

1. 라디안과 호도법

 

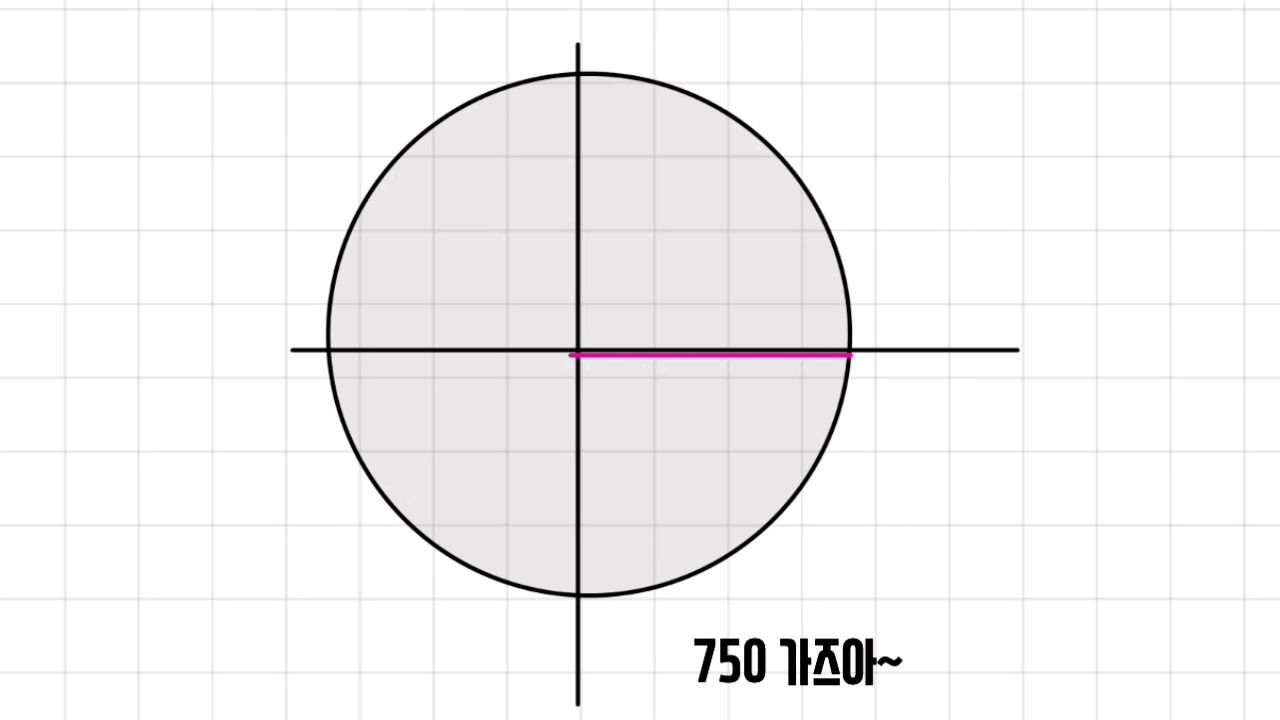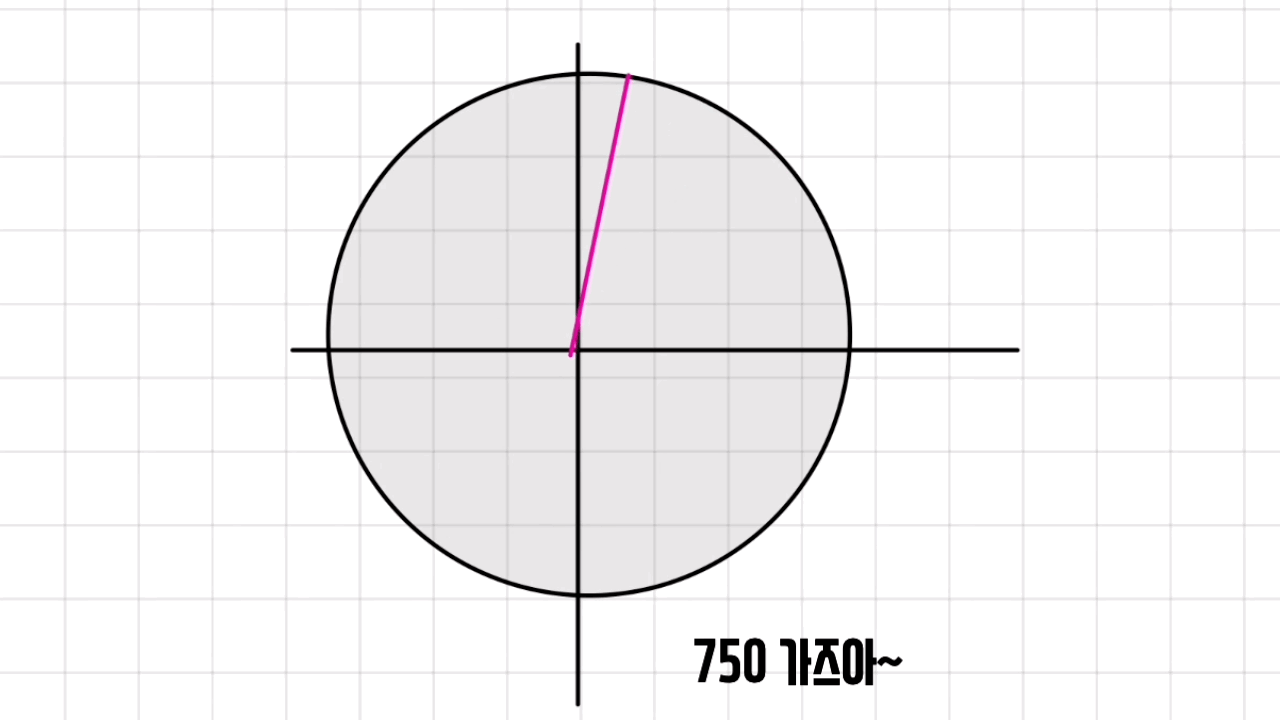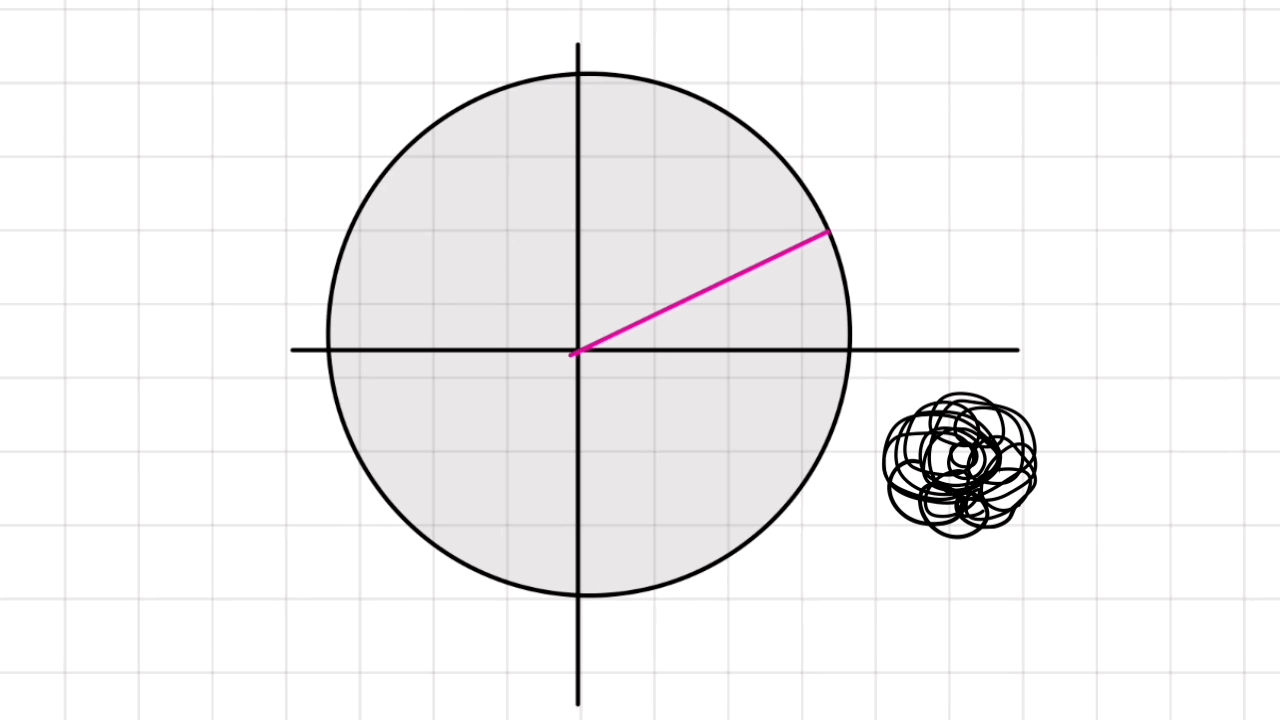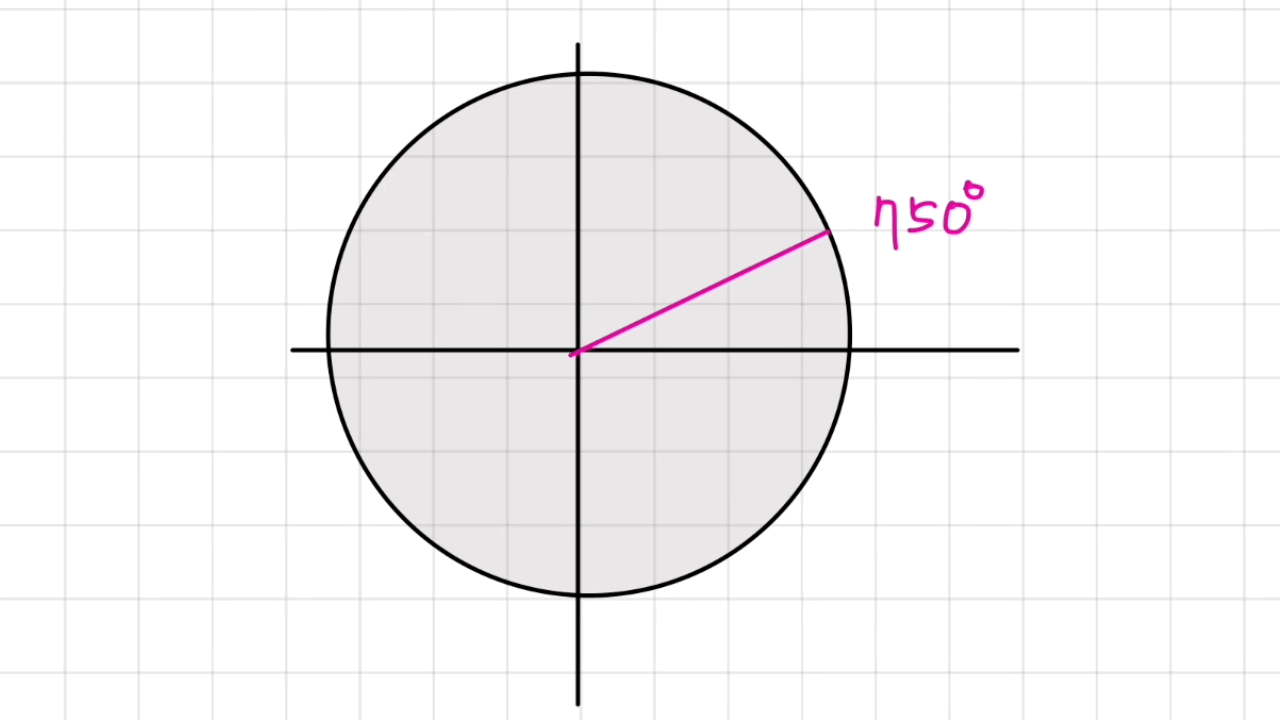
시초선으로 부터 750도를 회전 한 방향을 떠올려 보자. 자주 접해본 각이 아니라서 직관적으로 어떤 방향인지 바로 떠오르지는 않을 것이다. 그래서 앞서 공부했던 일반각을 통해 750도는 360도를 몇 번 반복하고 알파를 찾는 번거로움을 수행해야 한다. 아래의 그림은 750도를 찾는 것을 이미지로 만들어 본 것이다.

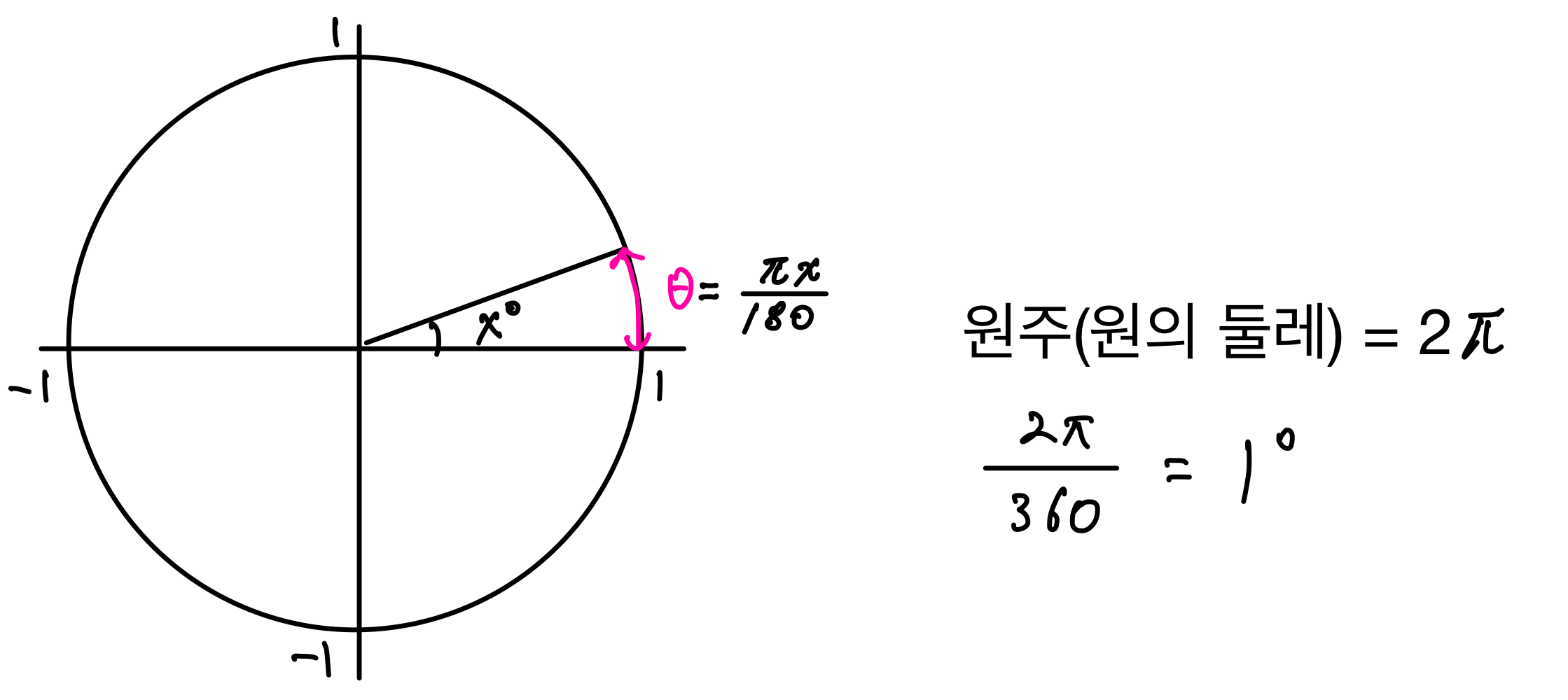
그렇다면 직관적으로 쉽게 방향을 찾을 수 있는 방법이 있다? 그렇다!! 바로 라디안을 이용한 방법은 동경의 방향을 쉽게 찾을 수 있게 해준다. 라디안을 공부하기 위해서 아래의 정의에 대한 의미를 익혀보자.

 

라디안의 정의 : 반지름의 길이가 1인 원의 중심각에 대응하는 호의 길이

반지름의 길이가 1인 원의 둘레를 360개로 나눴을 때 길이는 1도에 대응하게 된다. 따라서 1 Radian은 아래의 그림과 같이 표현 될 수 있다.

특수각과 라디안

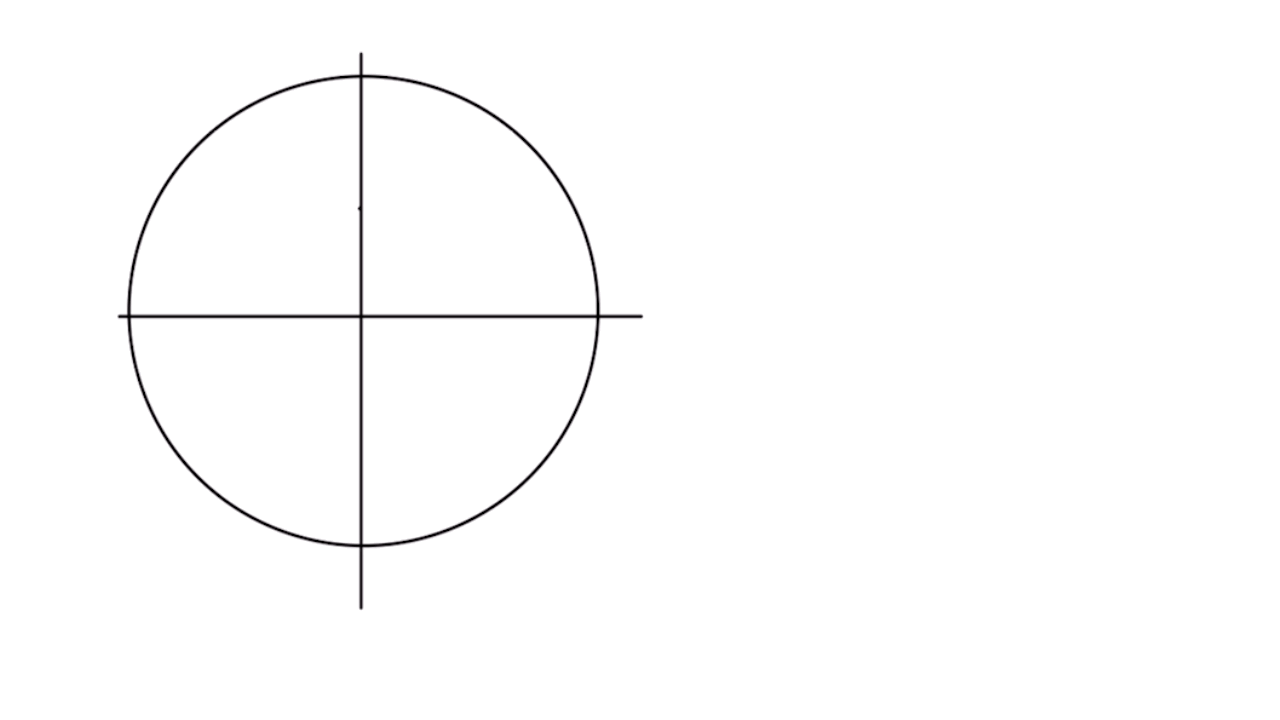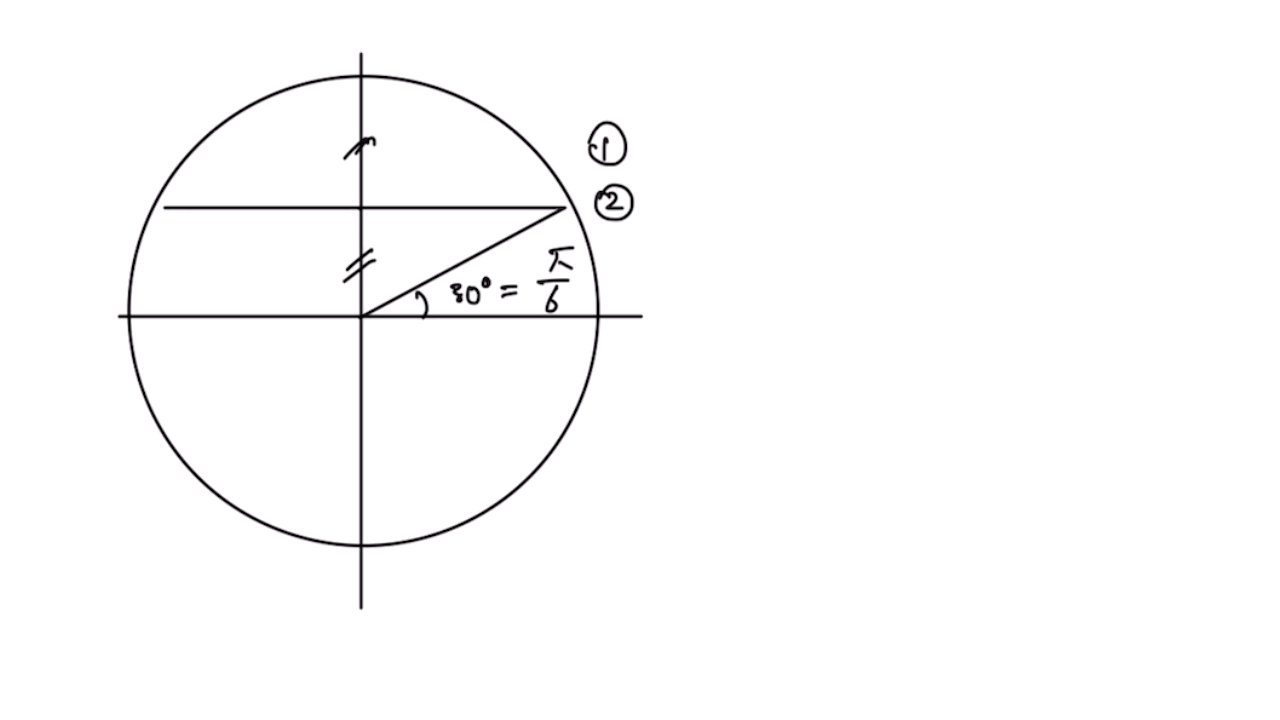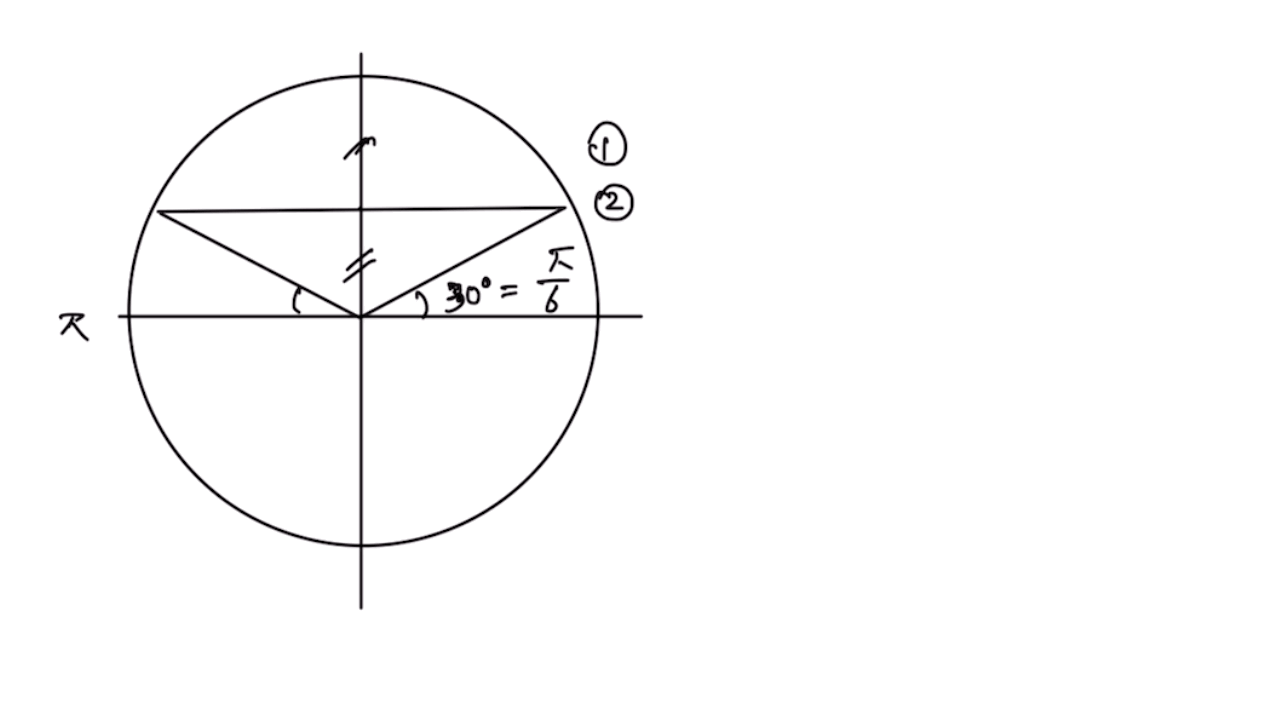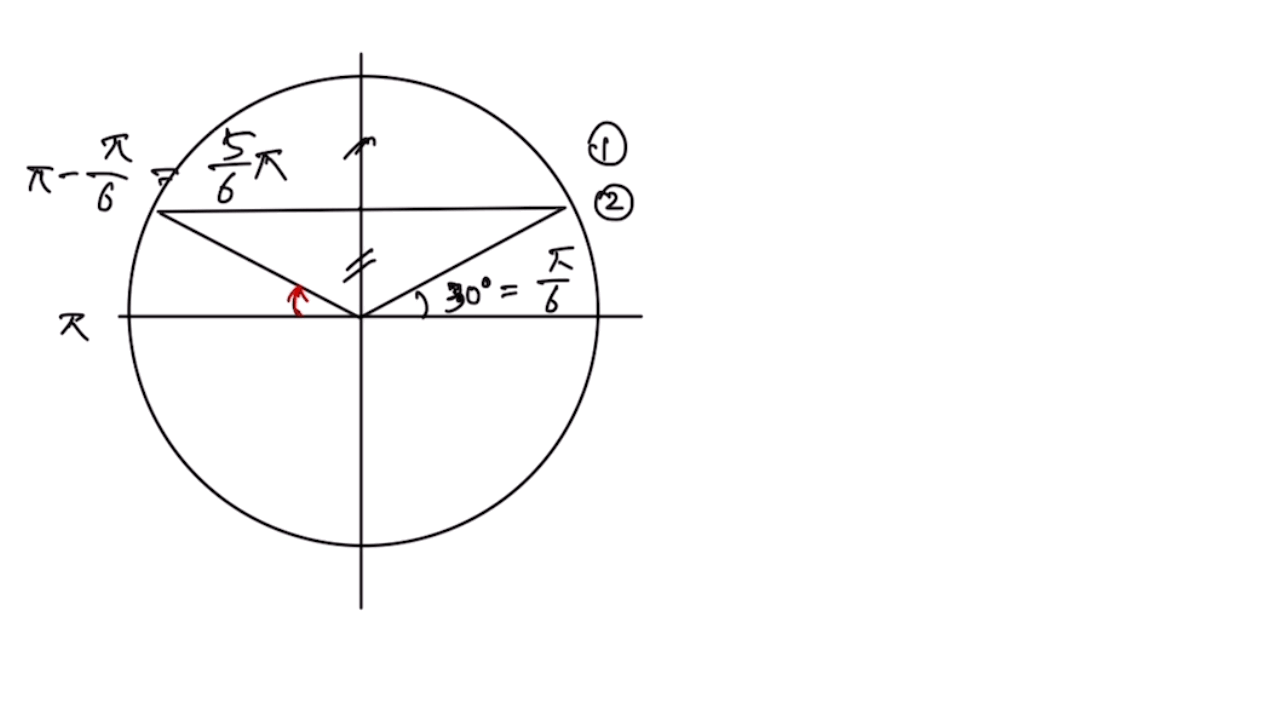
현행 고등 과정에서 가장 많이 사용하는 각도 30, 45, 60 의 배수는 반드시 익혀놓아야 다음 사인 코사인 탄젠트의 값을 찾는데 유용할 수 있다. 원을 이용해 특수각을 찾는 요령은 다음과 같은 방법을 따르면 된다. 

ㄱ. 30도의 배수 라디안 및 위치

ㄴ. 45도의 배수 라디안 및 위치

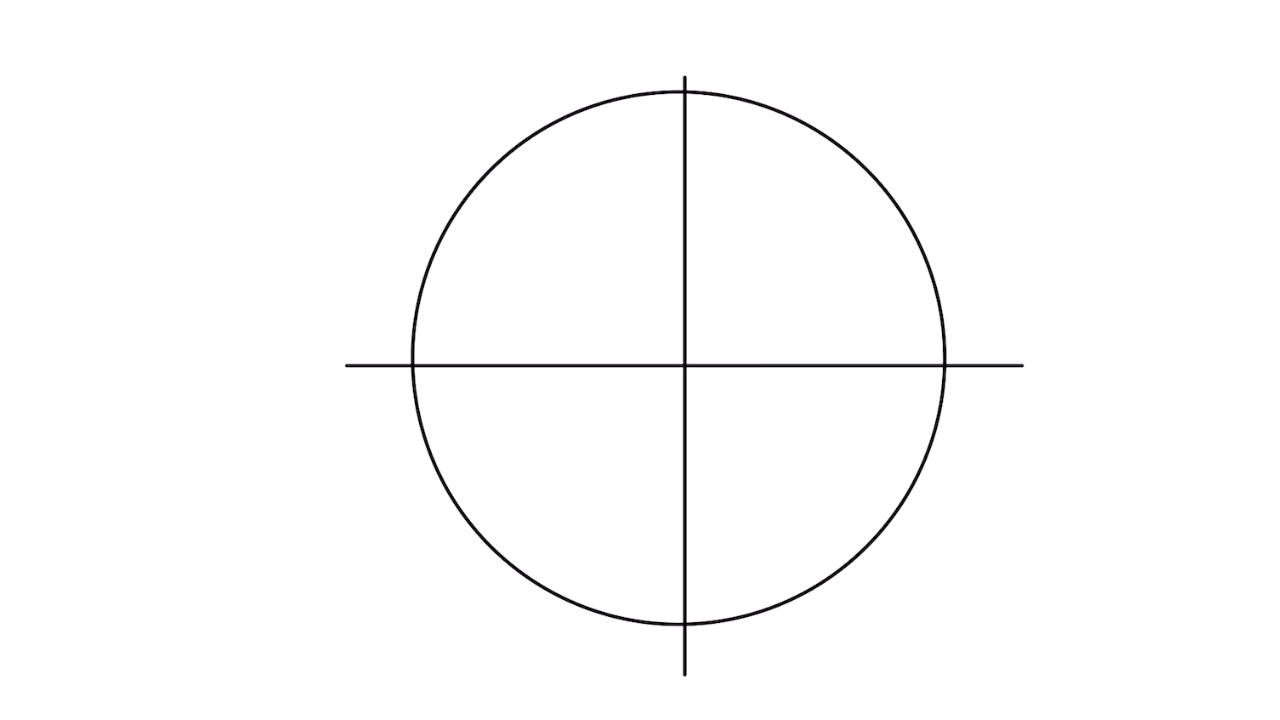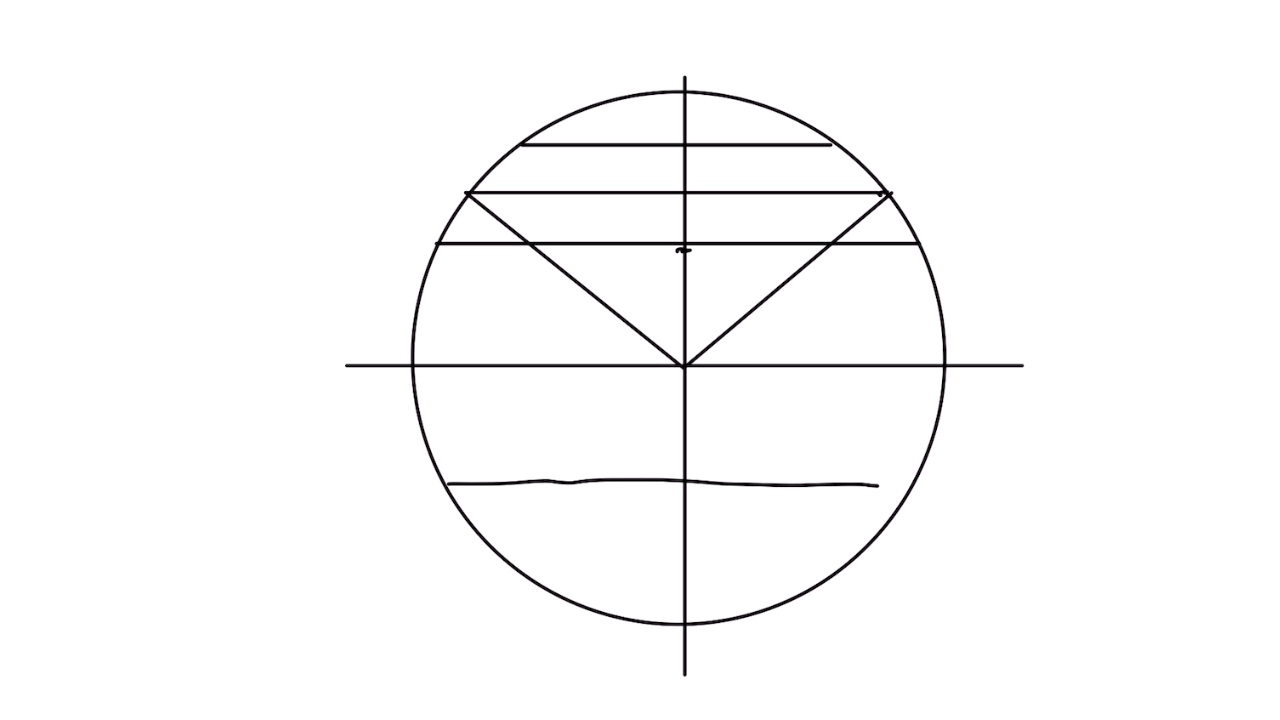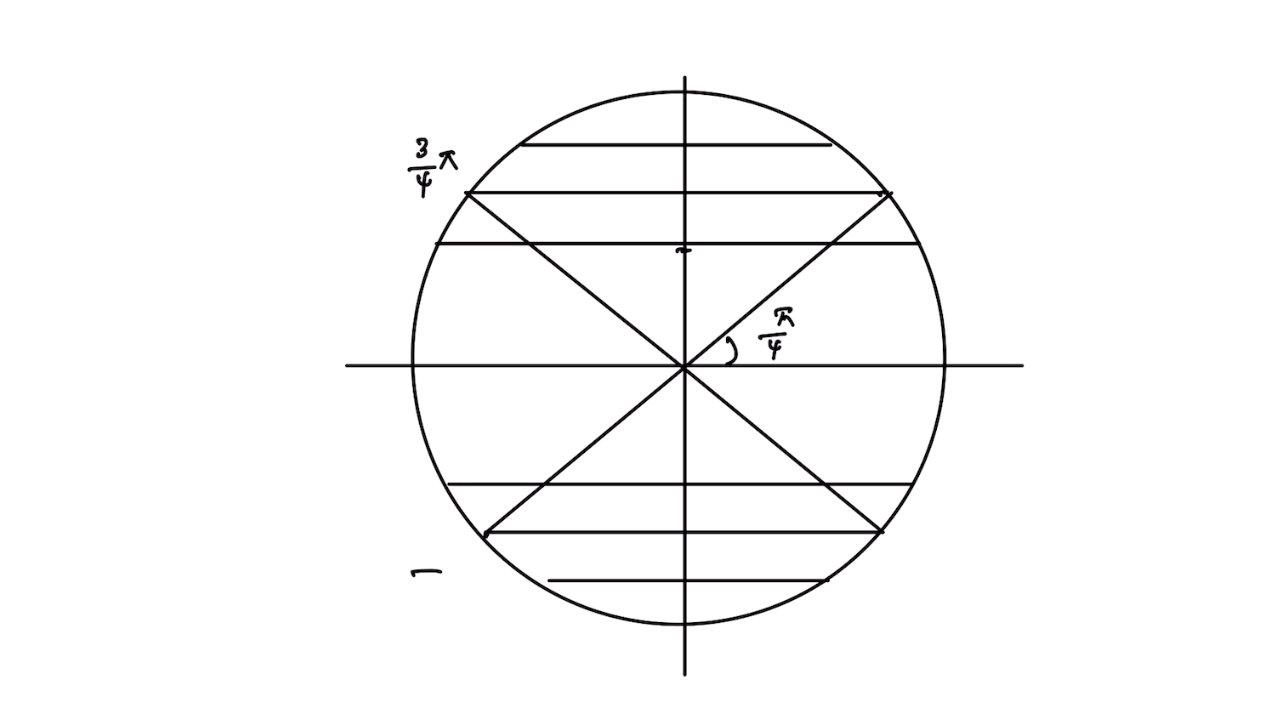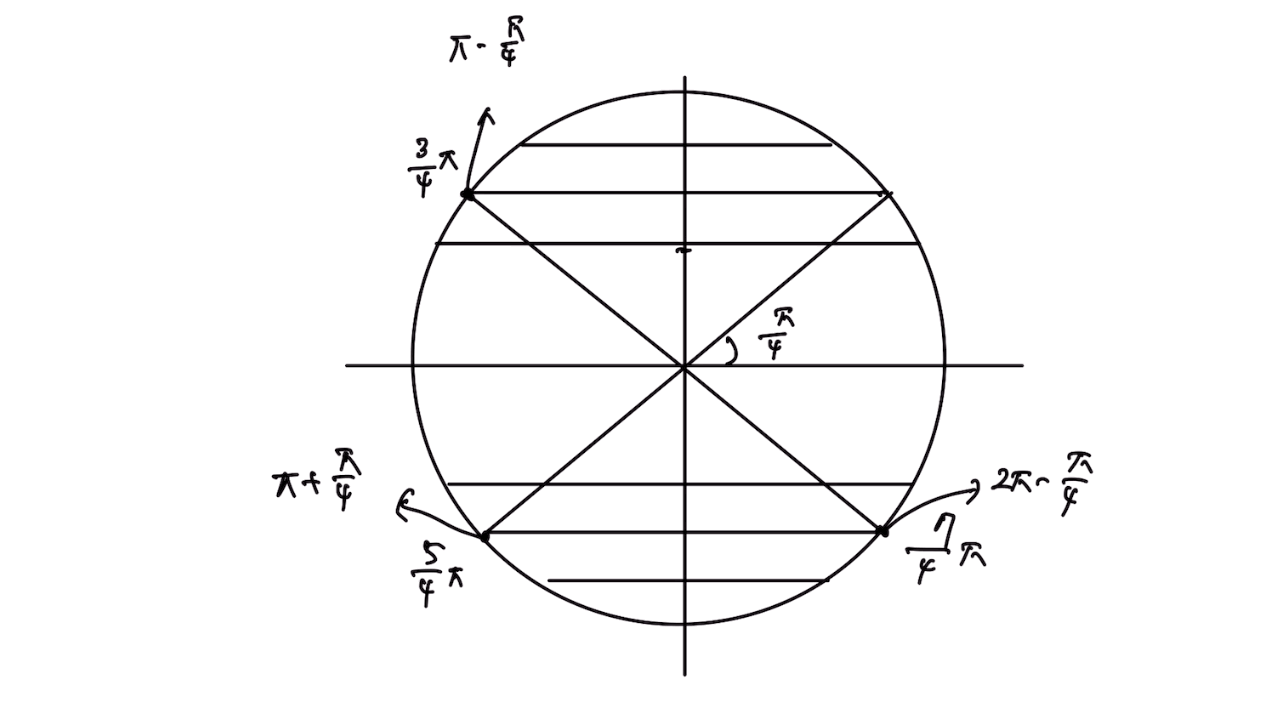
ㄷ. 60도의 배수 라디안 및 위치

2.  부채꼴의 호의 길이와 넓이

(중심각의 크기가 같은 부채꼴은 모두 닮음이다! 닮음은 위대하다!)

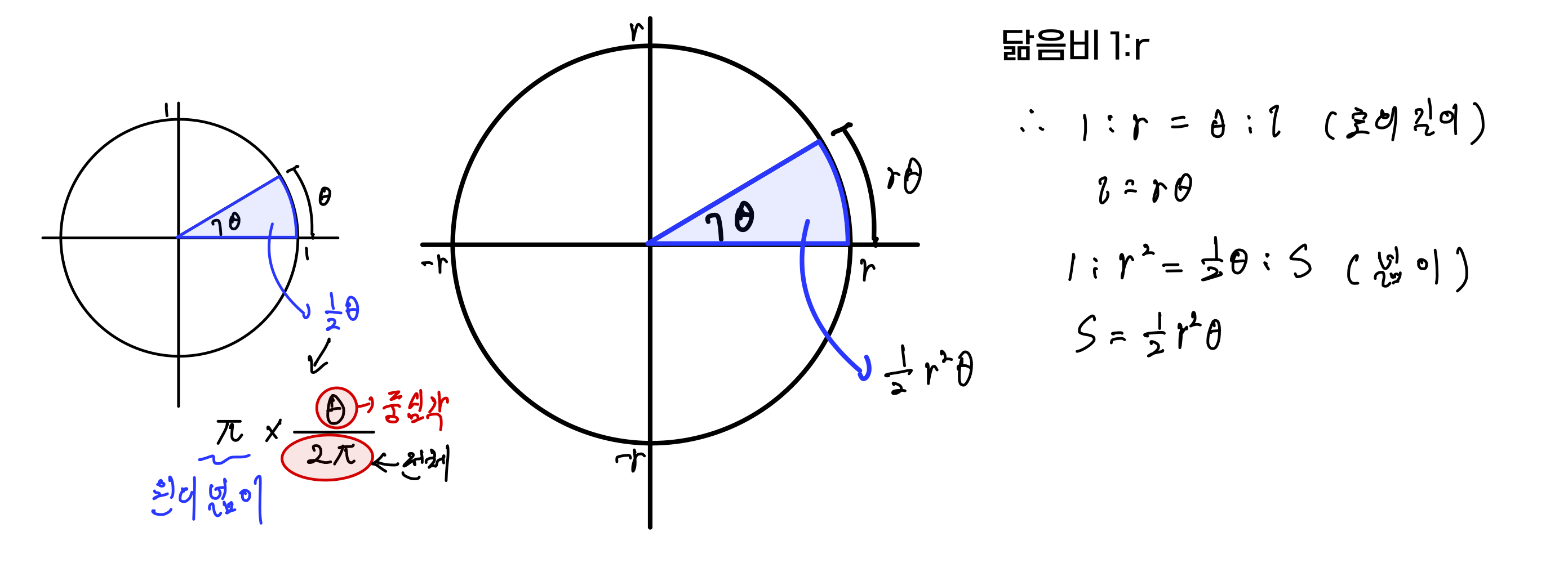
반지름 길이가 1인 원의 중심각의 크기가 세타가 되는 부채꼴의 넓이를 라디안으로 표현하면 다음과 같다. 우선 반지름 길이 1인 원의 넓이는 파이가 되며 이 값에 전체 원에서 차지하는 비율을 곱하면 부채꼴의 넓이가 된다. 전체 원의 둘레길이는 2파이가 되며 중심각의 크기가 세타가 되므로 전체 비율은 세타/2파이 가되어 위 그림과 같이 넓이는 1/2 세타가 된다. 이를 이용해 닮음비를 이용하면 어떤 임의의 반지름을 가진 원의 넓이를 표현할 수 있다.

 

<예시문항> (이미지를 클릭하면 해설영상으로 연결됩니다)